礦車通常由機車牽引,運行于窄軌之上,它可以有效地將所開采礦石及矸石運輸到指定位置,是一種優良的巷道及井下運輸設備。按其結構和卸載方式不同,礦車可分為單側曲軌側卸式礦車、固定式礦車、翻斗式礦車、底(側)卸式礦車和梭式礦車5大類。其中,單側曲軌側卸式礦車是使用頻繁的一種礦山運輸設備,其特點是機構復雜,卸載曲軌通常為空間螺旋線,如用傳統方法設計,必須通過物理樣機來驗證其設計方案的可行性,導致設計過程漫長且費用較高。利用虛擬樣機技術對礦車的運動過程和力學特性進行計算機仿真,力求獲得滿足實際需要的卸載系統,對于提高礦車研發效率、降低研發風險、控制設計成本等具有不可替代的積極作用。
1 工作原理
如圖1所示,2m3單側曲軌側卸式礦車的工作原理是在機車牽引下,礦車沿軌道向前運行,卸載推桿通過曲軌過渡裝置時,首先使卸載推桿的間隙消除,當推桿通過曲軌自卸段時,車廂開始繞底盤上的轉軸回轉;與此同時,車廂門的鎖鉤在其開起機構挺桿的作用下開始回轉,當車廂傾轉達到一定的角度時,鎖鉤與側門脫開,側門開起并卸礦。
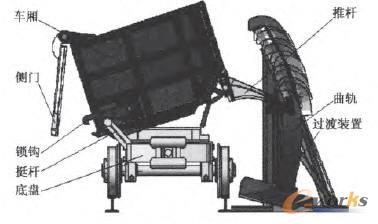
圖1 單側曲軌側卸式礦車
隨著礦車向前運行,推桿被曲軌的表面逐步抬高,車廂繼續翻轉,卸載角不斷增大到最大,并保持一段距離,使礦石傾瀉而出;然后,推桿進入曲軌的復位段,礦車各部動作與卸載時剛好相反,側門在自重作用下逐漸關閉,鎖鉤復位鉤住側門,完成一次卸載過程。由于卸載過程中礦車受力狀況復雜,整個礦車要承受較大的沖擊載荷,因此卸載能否順利進行在很大程度上取決于曲軌的形狀和推桿的形狀位置尺寸。曲軌形狀的設計及推桿形狀位置尺寸的合理與否,將直接關系到礦車卸載的平穩性和使用壽命。
2 礦車設計
礦車的推桿在曲軌上運行,其運行的平穩性主要由曲軌的外形決定。為保證推桿不在曲軌上發生側滑,理論上要求曲軌的工作表面應和推桿在卸載的任何時刻都保持垂直,不產生任何附加彎矩;因此,曲軌設計顯得尤為重要,其形狀的好壞直接關系到礦車工作時是否產生沖擊,是否安全可靠。2m3單側自卸式礦車的曲軌曲線及曲軌如圖2所示。
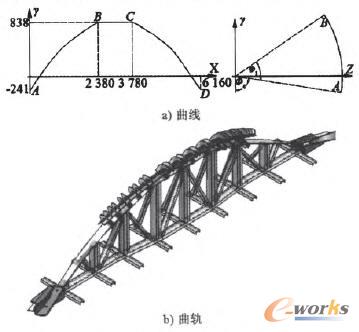
圖2 曲軌曲線及曲軌
推桿裝置的形狀尺寸及其在車體上的安裝位置在礦車卸載過程中占有重要的地位,推桿裝置設計應注意以下2種情況:1)推桿滾輪的回轉軸線必須始終與車廂卸載回轉軸相交,這樣可以保證卸載過程中推桿滾輪面始終與曲軌面垂直,且不產生側滑;2)推桿軸的安裝位置必須與車廂卸載回轉軸位置、曲軌形狀及推桿幾何形狀相匹配,這樣既能很好地完成卸礦,又能使其不與曲軌和頂桿裝置相干涉。如圖3所示為一典型的礦車推桿裝置。
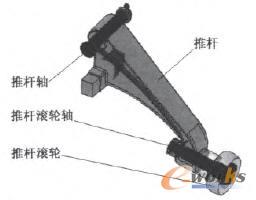
圖3 推桿裝置
2m3單側自卸式礦車的底盤如圖4所示,它是整個車體和礦物的承載結構和走行機構,其設計精度決定了礦車的整體功能;因此,必須對其加以認真仔細的研究。

圖4 底盤
礦車車廂如圖5所示,是礦物承載容器,車廂側門如圖6所示,車廂及側門均由熱軋型鋼和鋼板拼焊而成,它們之間的連接既要保證卸載時側門最大限度的開起,又要保證運輸時的可靠閉合。

圖5 車廂

圖6 側門
3 礦車自由度計算
在推桿裝置進入曲軌卸載段時,礦車系統可以簡化為如圖7所示的連桿機構,要使其具有確定的運動,原動件的數目必須等于機構的自由度數。礦車卸載屬空間機構問題,其自由度的計算需要考慮各構件的6個自由度。空間運動副主要包括Ⅰ級副~Ⅴ級副,其所提供的約束數目分別是1~5。設空間機構共有n個活動構件,p1個Ⅰ級副,p2個Ⅱ級副,p3個Ⅲ級副,p4個Ⅳ級副和P5個Ⅴ級副,則機構的自由度可表示為:
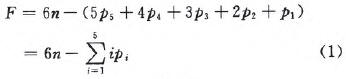
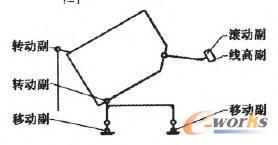
圖7 礦車各構件自由度圖
推桿裝置中滾輪的滾動副屬于虛約束,可以忽略,而底盤與鋼軌間的2個移動副具有相同的運動規律,可以看作是一個移動副。代入式1可得:
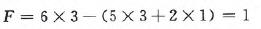
可見,整個礦車的自由度為1,系統具有確定的運動規律。
當推桿進入曲軌過渡段時,推桿與車廂間形成轉動副。當推桿通過曲軌過渡段進入卸載段后,上述轉動副消失,此時只需考慮礦車進入卸載段時是否對車體產生沖擊。
4 力學方程建立
如圖7所示為單側曲軌自卸式礦車多剛體動力學模型,在對其進行分析計算時,可不考慮構件的彈性變形,礦車運動過程中,須進行如下假設:1)系統構件都看作剛體,不考慮其彈性變形;2)運動副中無間隙和摩擦;3)構件的運動速度不高。
把構件所受外力及質量轉化到等效構件上,使其運動與機構的實際運動一致,并建立等效構件的動力學模型,據此,將復雜系統的動力學問題看作是等效構件的動力學問題來求解。
4.1 等效力與等效力矩
根據功能原理,等效力和等效力矩所做功與外力或外力矩所做功應該相等。設Fk(k=1,2,…,m)和Mj(j=1,2,…,n)分別為作用在礦車系統上的外力和外力矩,根據等效力Fe和等效力矩Me的功率與機械系統的總功率相等可得:
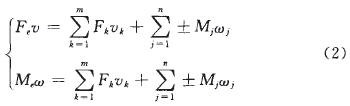
式中,ω為等效構件的角速度;v為等效構件的速度;vk為外力Fk作用點的速度;ωj為外力矩Mj作用在構件的角速度。
根據式2可求出Fe和Me的表達式為:
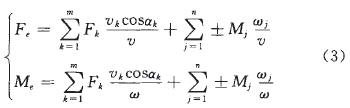
式中,αk為Fk與Vk的夾角。
從式3可以看出,等效力和等效力矩不僅與構件所受的外力和外力矩有關,而且還與其傳動比(ωj/v、vk/v(或ωi/ω、vk/ω)有關。
4.2 質心及轉動慣量確定
等效構件所具有的總動能是各構件的分動能之和,因此,做空間運動的構件所具有的動能為:
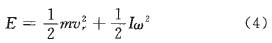
式中,m為構件的質量;I為構件相對于質心的轉動慣量;Vr為構件質心的速度;ω為構件的角速度。
對于做平動或定軸轉動的構件,式4可分別簡化為:
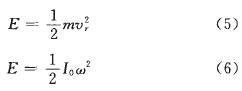
式中,Io為構件相對于其轉軸的轉動慣量。
根據動能相等的原則,等效構件的質量me和轉動慣量Ie應滿足:
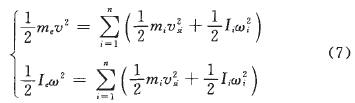
推導出的等效構件的質量me和轉動慣量Ie可表示為:
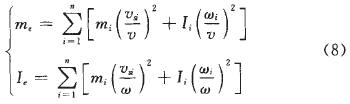
式中,vk為第i個構件質心速度;ωi為第i個構件角速度;n為活動構件數量。
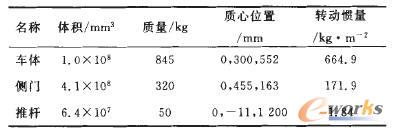
據此可確定礦車系統的質心及轉動慣量。由于計算過程簡單而繁復,因此本文僅給出計算所得的結果,具體數據見表1。
表1 各部件的質量分布及相關數據
4.3 動力學方程建立
取單個礦車為研究對象,卸載軌道內外礦車底盤的運動規律相同,且僅做平動;卸載段和復位段間的直線段距離為1.4m;鼓形推桿滾輪和卸載曲軌間為光滑接觸,且在其上做純滾動。
根據動力學普遍方程,可得出多剛體系統的動力學方程為:
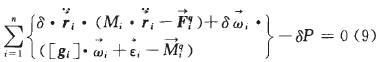
式中,
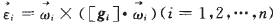
Mi為剛體i的質量;[gi]為剛體i的中心慣性張量;ri為剛體i的質心矢徑;ωi為剛體i的轉動角速度;δP為系統內力所完成的虛功率以及解除約束后的約束反力所做的虛功率總和;Fqi為作用在剛體i的外力主矢;M為作用在剛體i的相對質心的主矩,則其矩陣形式為:
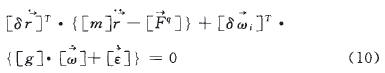
式中,
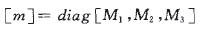
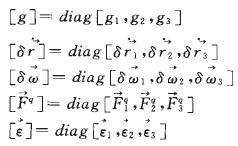
5 礦車穩定性校核
礦車車廂未翻轉時,可把推桿裝置、車廂和掛鉤看作整體,而側門看作是一個部件。其重心位置如圖8所示,坐標系見表2。
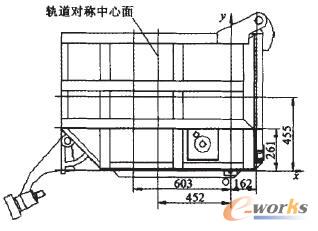
圖8 礦車原始狀態重心位置
表2 礦車未翻轉時的重心坐標
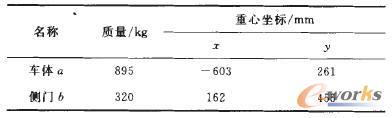
當車廂圍繞其回轉中心轉過40°時,車廂側門打開,通過坐標轉換求得車廂在最大翻轉角度時礦車的重心坐標。
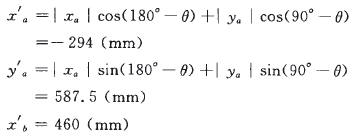
整個車廂在回轉40°時的重心橫坐標為:
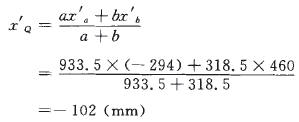
回轉中心距2條軌道對稱中心面的水平距離是452mm,軌距是973.5mm,則973.5/2-(452-102)=136.75(mm)。由此可見,當車廂翻轉40°時,整個礦車距右邊軌道內側的距離為136.75mm,礦車不會產生傾翻;因此,礦車是穩定的。
6 結語
以單側自卸式礦車為研究對象,對其性能進行了理論分析,綜合運用三維CAD軟件,建立其虛擬樣機模型,然后進行了運動分析。運用虛擬樣機技術對單側曲軌自卸式礦車進行了研發,建立了其虛擬樣機模型,為后續的分析奠定了基礎。研究了該礦車的主要部件及各部分的作用,并對其關鍵的零部件進行了分析。基于單側曲軌自卸式礦車的主要工況,建立了其力學方程。對該型礦車的穩定性進行了校核。
核心關注:拓步ERP系統平臺是覆蓋了眾多的業務領域、行業應用,蘊涵了豐富的ERP管理思想,集成了ERP軟件業務管理理念,功能涉及供應鏈、成本、制造、CRM、HR等眾多業務領域的管理,全面涵蓋了企業關注ERP管理系統的核心領域,是眾多中小企業信息化建設首選的ERP管理軟件信賴品牌。
轉載請注明出處:拓步ERP資訊網http://m.kaqidy.com/
本文標題:單側自卸式礦車研究